پیوند ها
نظرسنجی سایت
آمار بازدید سایت
حل معادلات دیفرانسیلی پاره ای(PDE) و معمولی(ODE) به کمک روشهای صریح،ضمنی،تحلیلی و رانگ-کوتای مرتبه 2 و 4 به کمک کد نویسی نرم افزار MATLAB
اكثر پديده هاي مهندسي در زمينه هاي ترموديناميك،ديناميك سيالات،الكتريسيته،مغناطيس،مكانيك و انتقال حرارت و... با معادلات ديفرانسيل پاره اي توصيف مي شوند.يك معادله ديفرانسيل پاره اي،معادله اي است كه شامل مشتقات جزئي باشد.تفاوت آن با معادلات ديفرانسيل معمولي در اين است كه تابع وابسته به چند متغيير مستقل مي باشد.به منظور حل اين دسته از معادلات روشهاي مختلف تحليلي وجود دارد،اما در بسياري از مسائل به كمك روشهاي تحليلي نمي توان پاسخ نهائي سيستم مد نظر را محاسبه نمود؛لذا در در اينگونه مسئله به منظور محاسبه پاسخ نهائي،روشهاي عددي مورد استفاده قرار مي گيرد.در اين پروژه سعي شده است كه معادلات ديفرانسيل پاره اي سهموي به روش تفاضلات محدود،روش صريح، روش ضمنی شرح داده شود و مثالهائي براي آن حل شود كه اصلي ترين مثال اين روش،حل توزيع دما مي باشد.
سوال:
مقدار (y(xرا برای شرایط زیر با استفاده از روش رانگ کوتای مرتبه2 و4به دست آورید؟
0.5y"+10y+100y=0 y(0)=1 ,y(0)=0 ,0<x
توجه :
حل مساله بالا به همراه کدنویسی های آن به طور کامل و به صورت کدهای عمومی که میتوان آن را برای حل هر مساله ای با هر اعدادی حل نمود، همچنین رسم نمودار های مختلف در مکانها وزمانهای مختلف در فایل هایword نوشته شده است که شما عزیزان کافی است آن را در پنجره editor نرم افزار متلب کپی کنید و آنرا اجرا و جواب مساله خود را دریافت نمایید.
Runge-Kutta Method of Order 4
روش رانگ-کوتای مرتبه 4 یکی از روش های انتگرال گیری عددی از معادلات دیفرانسیل معمولی (ODE) است که برای حل معادلات به شکل
مورد استفاده قرار می گیرد. در این روش داریم:
![y_{i+1}=y_i+{1/6}delim{[}{k_1 + 2 k_2 + 2 k_3 + k_4}{]}](https://liberica.org/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_983_0285246f287427c860229e657455a3d9.png "y_{i+1}=y_i+{1/6}delim{[}{k_1 + 2 k_2 + 2 k_3 + k_4}{]}")
که در آن
هنگامی که تابع 
تنها تابعی از 
باشد روش رانگ-کوتای مرتبه چهار به روش انتگرال گیری سیمپسون تبدیل می شود.
(Runge-Kutta Method of Order 2)
Modified Euler Method
روش اویلر اصلاح شده (Modified Euler Method) یا همان رانگ کوتای مرتبه 2 یکی از روش های عددی برای حل معادلات دیفرانسیل معمولی به شکل
است. در این روش مشتق اول تقریبی مستقیم از شیب تابع در نقطه ی 
ارائه می دهد:
که 
تابع سمت راست تساوی معادله ی دیفرانسیل است که با 
مقدارگذاری شده است. اکنون با داشتن مقدار اولیه ی تابع 
، به کمک رابطه ی اویلر اصلاح شده می توان مقدار تابع را در گام های بعد محاسبه نمود:
![y_{i+1}=y_i+{h/2}delim{[}{f(x_i,y_i)+f(x_{i+1},y_i + hf(x_i,y_i))}{]}](https://liberica.org/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_ea7dcc416b2516b84acd7c575b3388f1.png "y_{i+1}=y_i+{h/2}delim{[}{f(x_i,y_i)+f(x_{i+1},y_i + hf(x_i,y_i))}{]}")
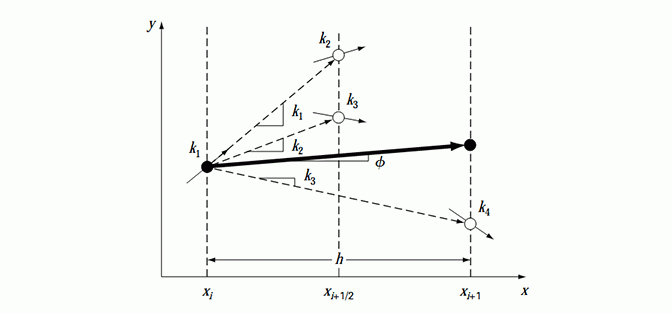
در تصویر زیر می توانید اثر استفاده از فرمول اصلاح شده ی اویلر را در یک مثال حل شده مشاهده کنید:
توجه :
روش حل معادلات دیفرانسیل معمولی (ODE)به کمک متد رانگ کوتای مرتبه 2 ومرتبه 4 به همراه کدنویسی وبرنامه نویسی کامل این روشها برای حل کامل معادلات دیفرانسیل مرتبه اول ودوم ، همچنین رسم نمودارهای مختلف در دو فایل word به صورت واضح خدمت شما عزیزان ارائه شده است.
مبلغ واقعی 28,875 تومان 20% تخفیف مبلغ قابل پرداخت 23,100 تومان
برچسب های مهم
تهران
